# Clustering
- 비지도학습의 대표적인 예시가 클러스터링이다.
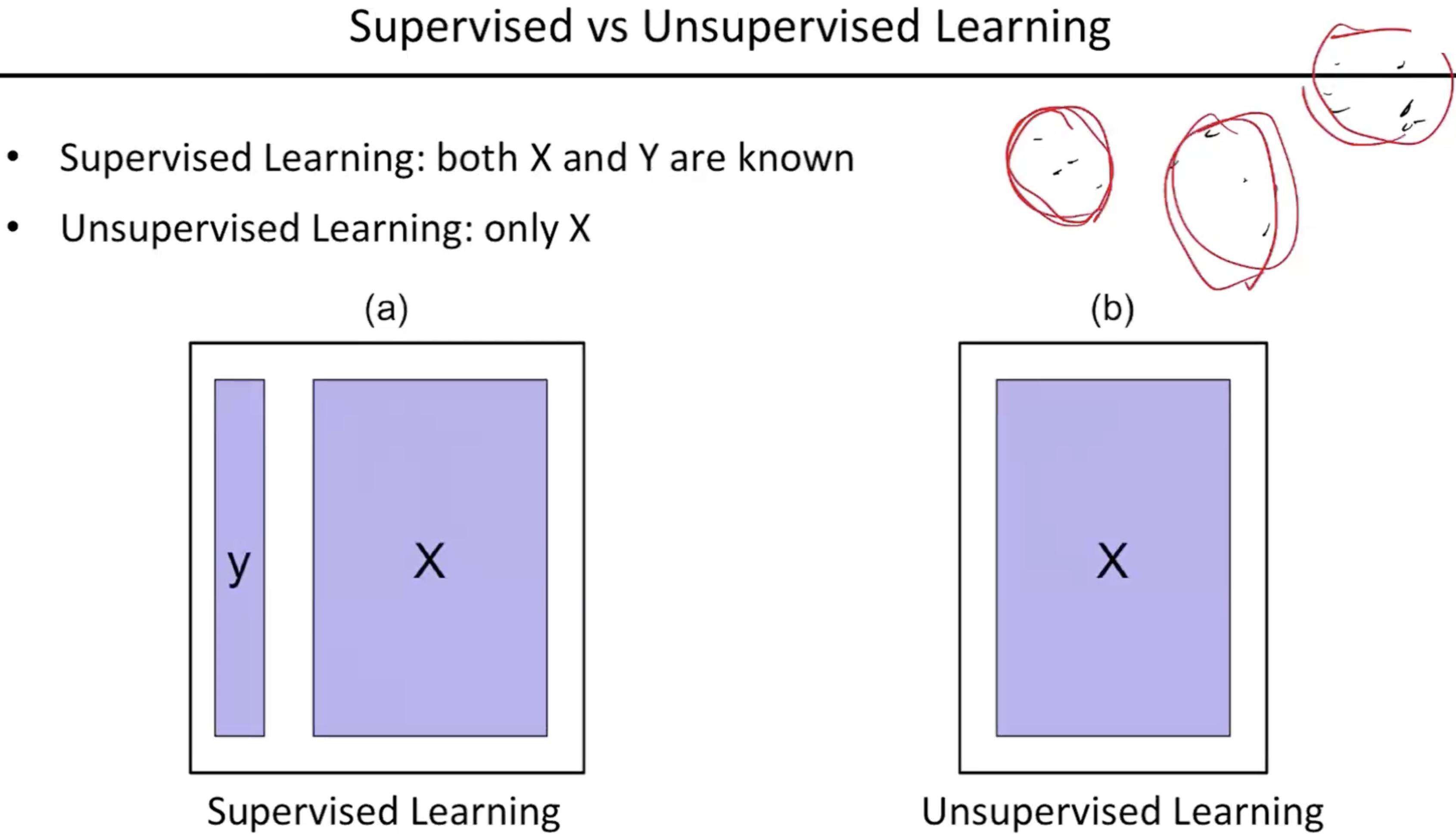
- 지도학습일때 레이블이 있기에 클러스터링은 더 쉽게 할 수 있다. 하지만 데이터가 많이 있는데 레이블을 따는것이 생각보다 돈과 자원이 많이 드는 행위이다. 그래서 그런 데이터가 존재하지 않을때 남아있는 학습 데이터만 가지고 어떤 유의미한 데이터를 뽑아내냐를 할 줄 아는것도 꽤나 중요한 task이고 그 중 하나가 클러스터링이다.

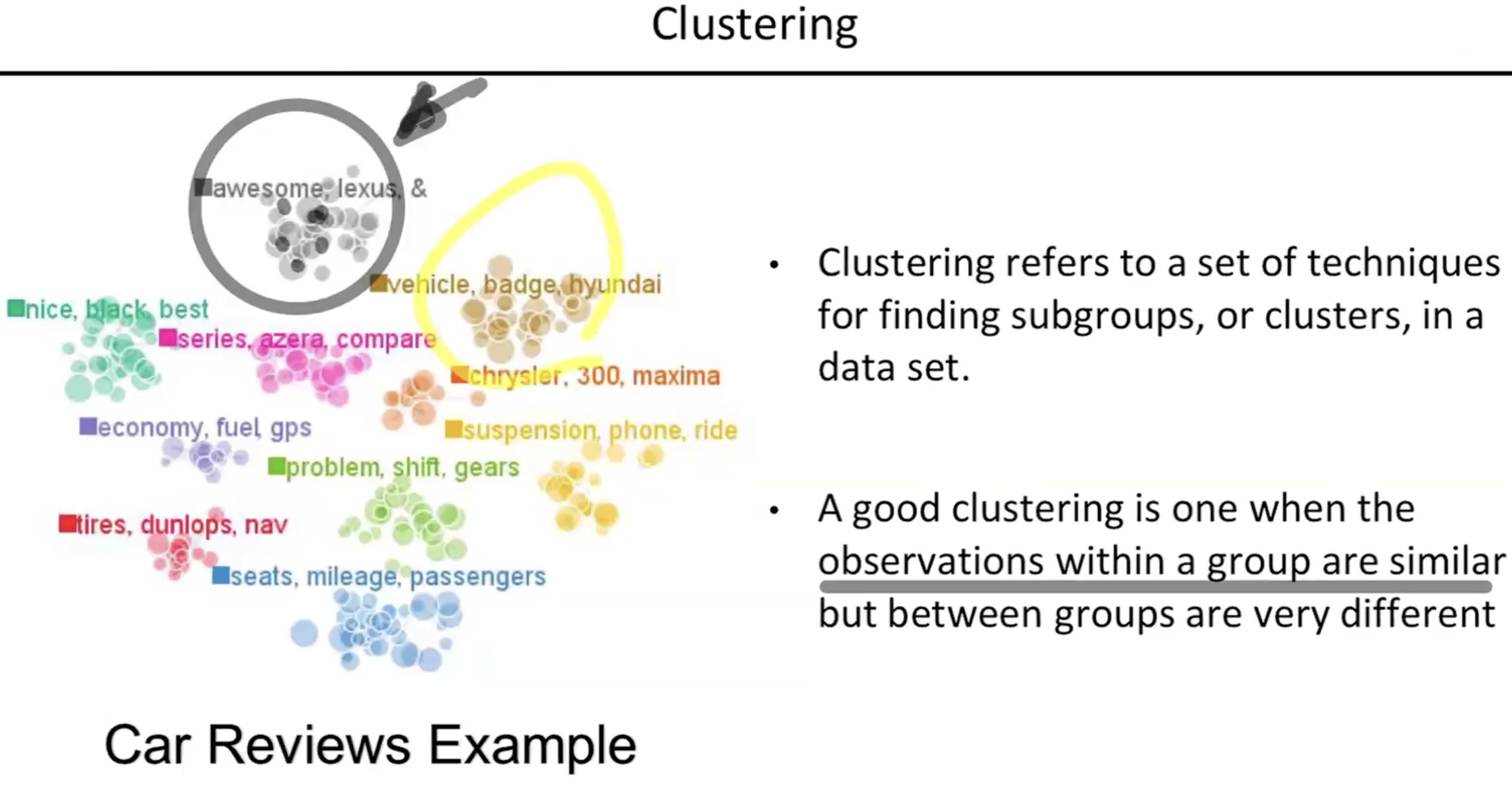
- 클러스터링은 데이터셋에서 서브그룹을 찾는 행위이다. 데이터들이 어느 군집을 이루는 같은 의미를 가지는 어떤 데이터의 특정군집을 이룰 수 있다는 그 기준을 찾아주는 걸 클러스터링이라고 한다.
- 클러스터링을 제대로 했다면 클라스안에 있는 데이터들끼리는 서로 비슷한 데이터가 있어야 한다. 다른 클러스터에 있는 데이터들끼리는 서로 다른 의미를 갖도록 클러스터화 하는것이 중요하다.
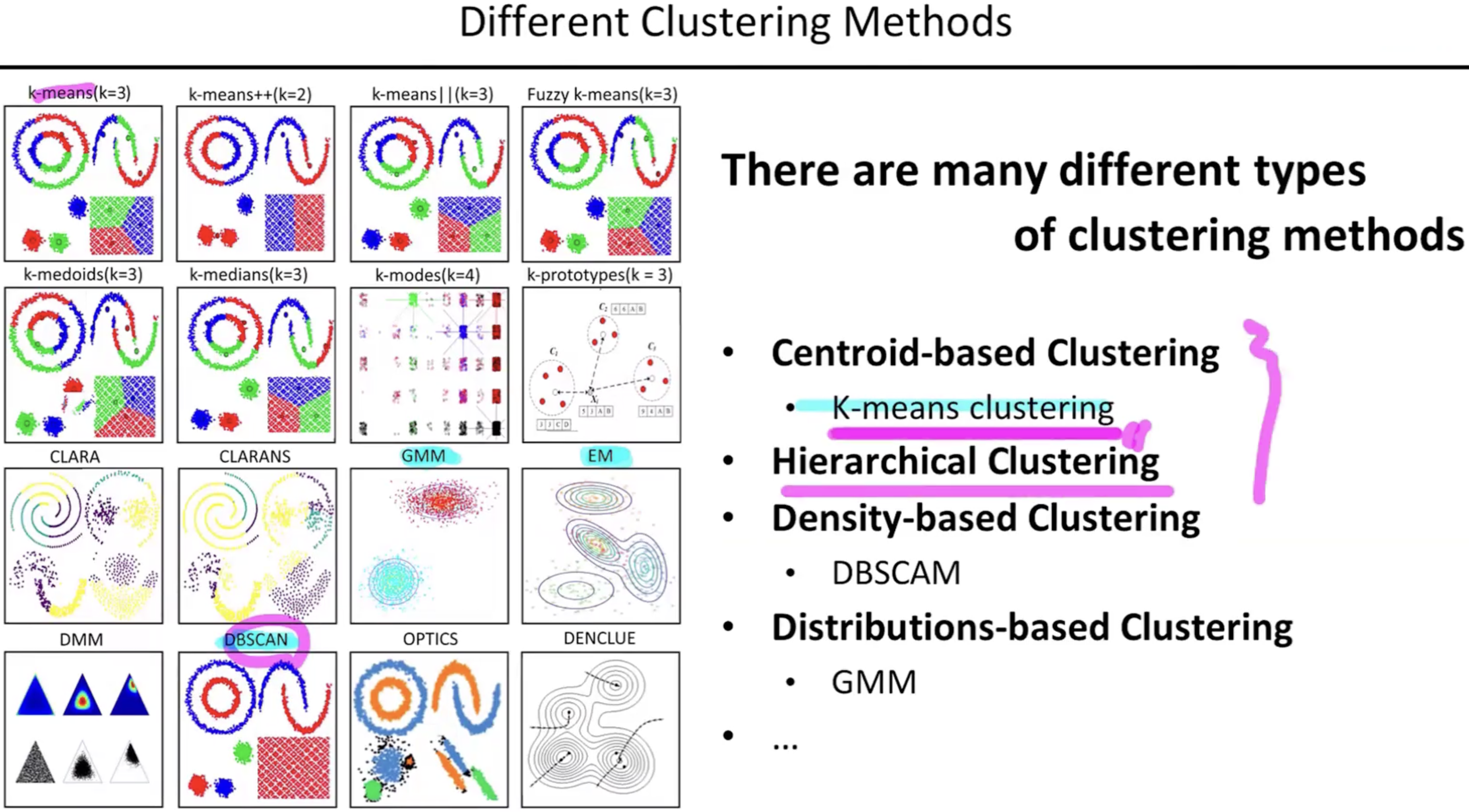
- 클러스터의 갯수를 정하고 시작한다.
# K-means Clustering
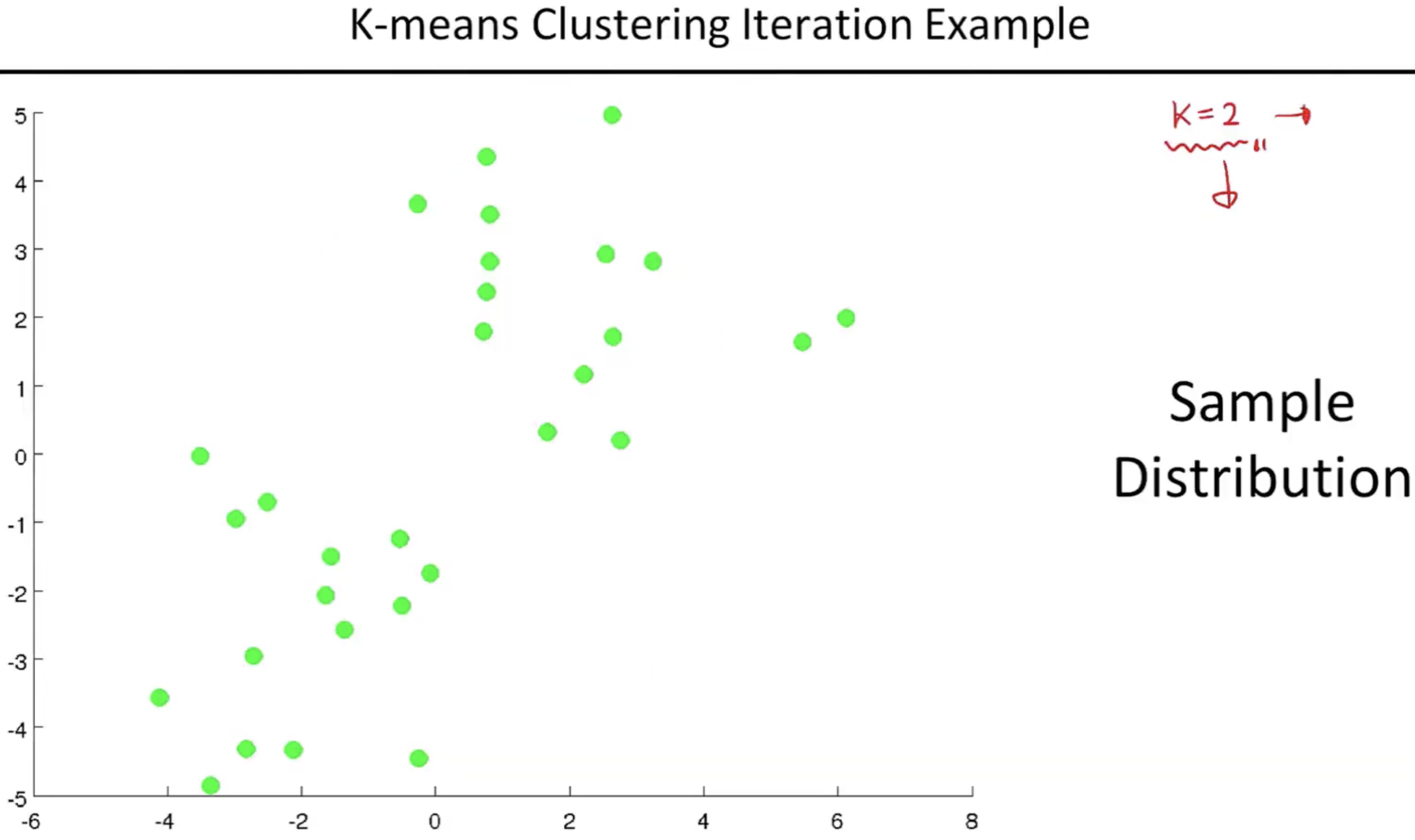
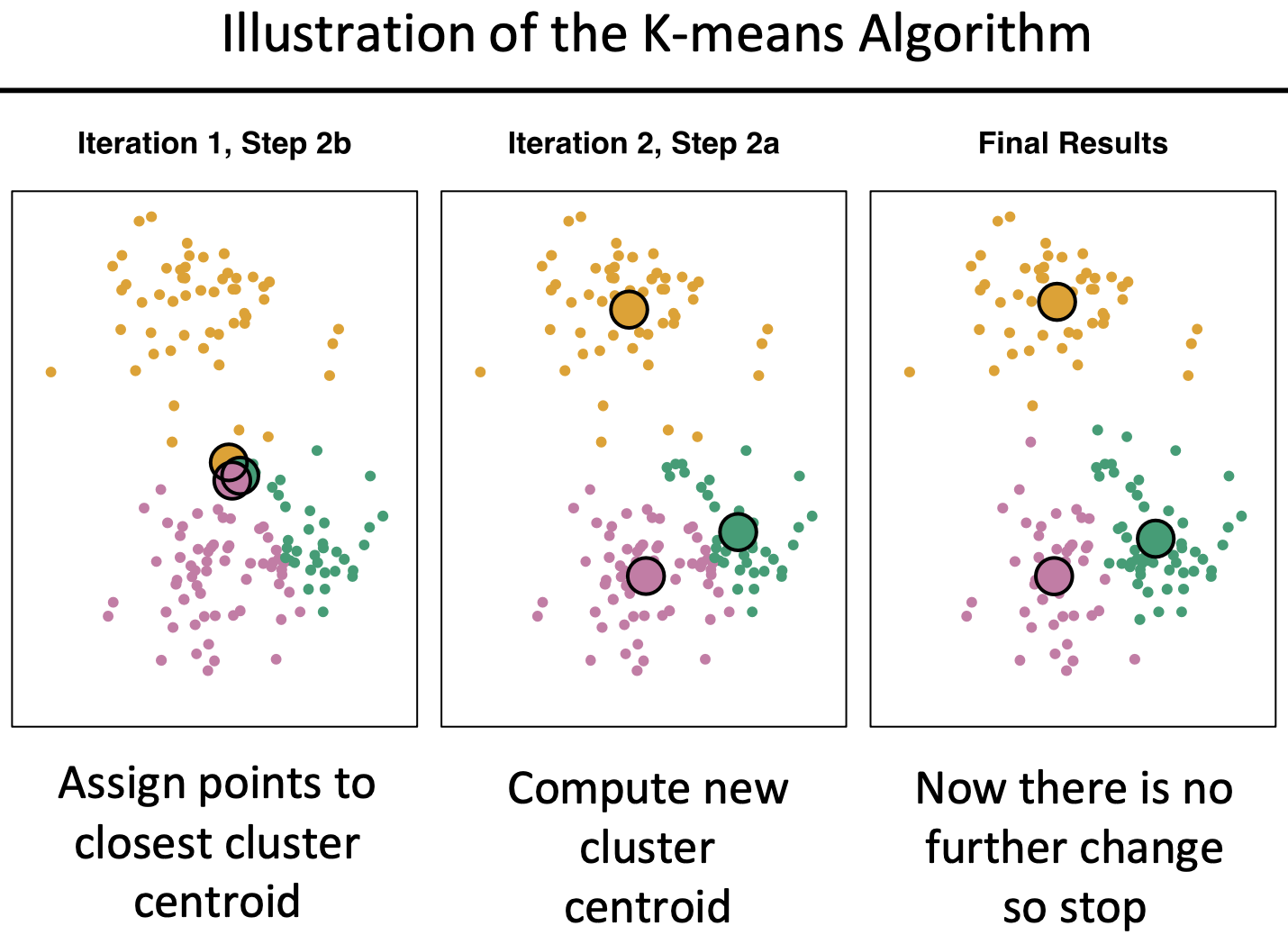
- 센트로이드를 아무곳에나 랜덤하게 찍는다. (예시로 아래 그림상에는 빨간색과 파란색 각각 하나씩)
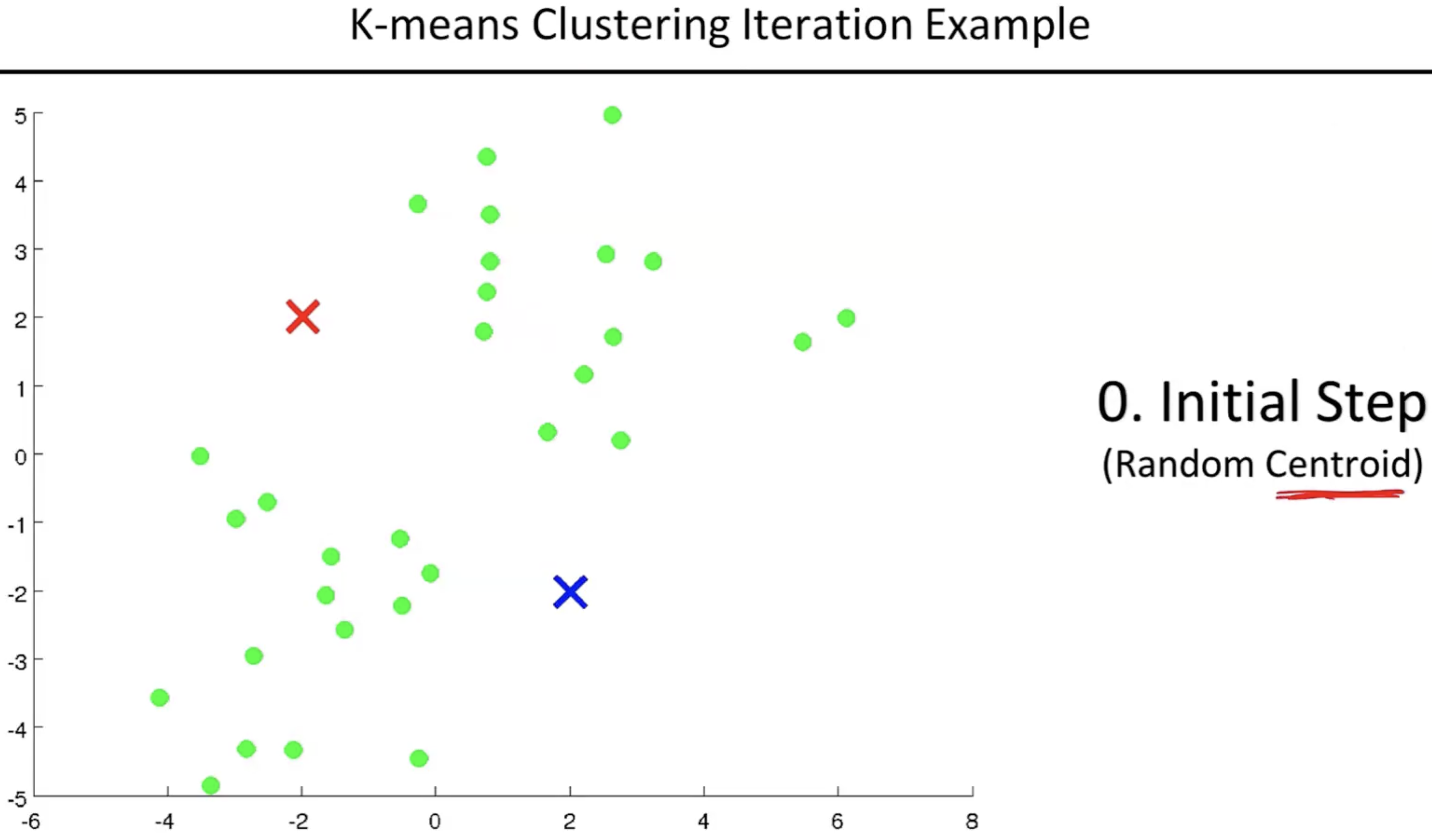
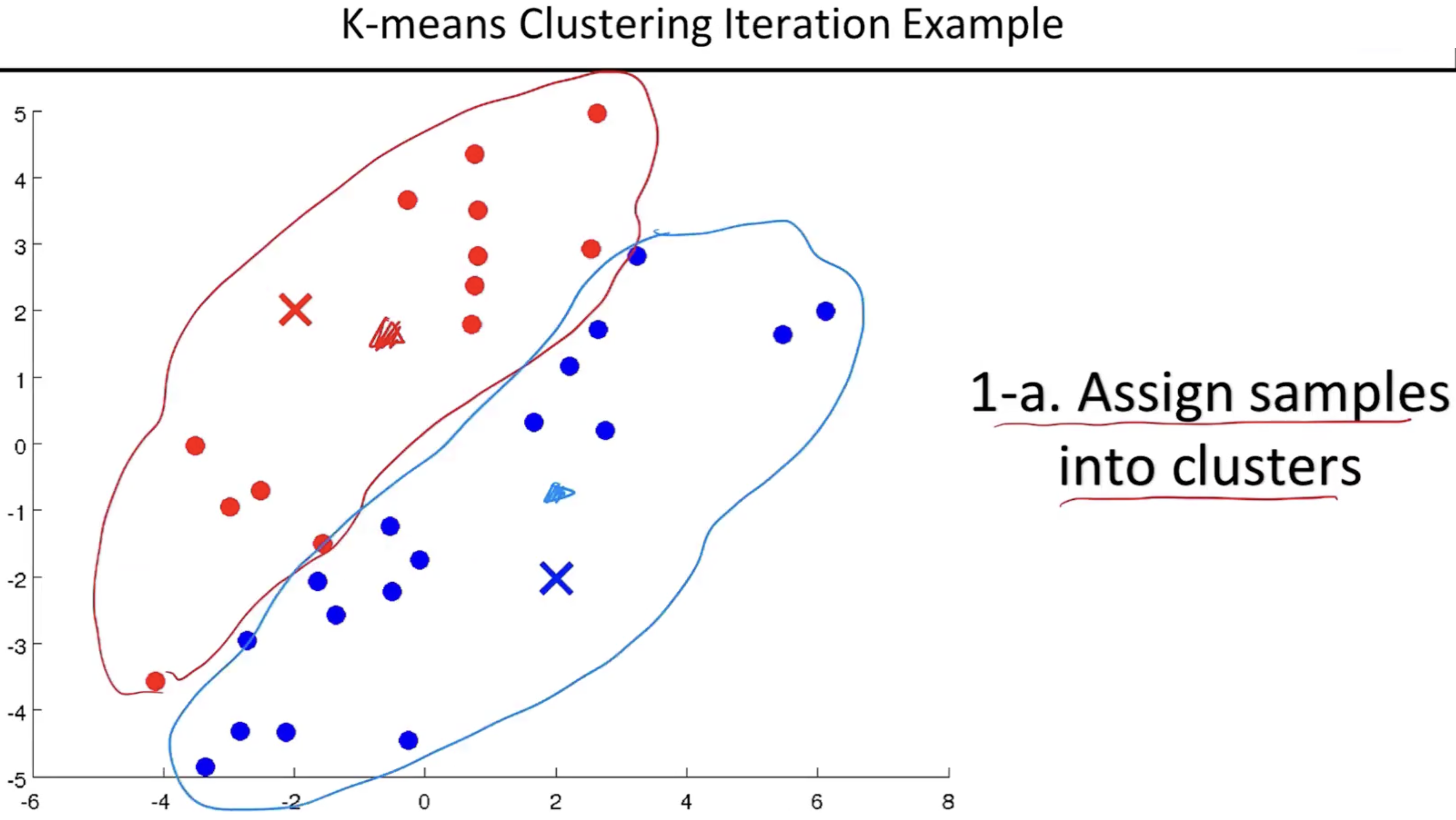
- 두 센트로이드를 기준으로 가까운 거리에 있는 데이터 포인트를 정하여 일차적으로 클러스터로 나눈다.
- 최적화된 클러스터의 갯수 구하는 방법은 따로 있기에 추후에 학습할 예정이다.
- 샘플을 클러스터로 일차적으로 나누는건 센트로이드에 해당되는 것을 랜덤하게 찍었기때문에 정확한 클러스터라고 말할 수 없다.
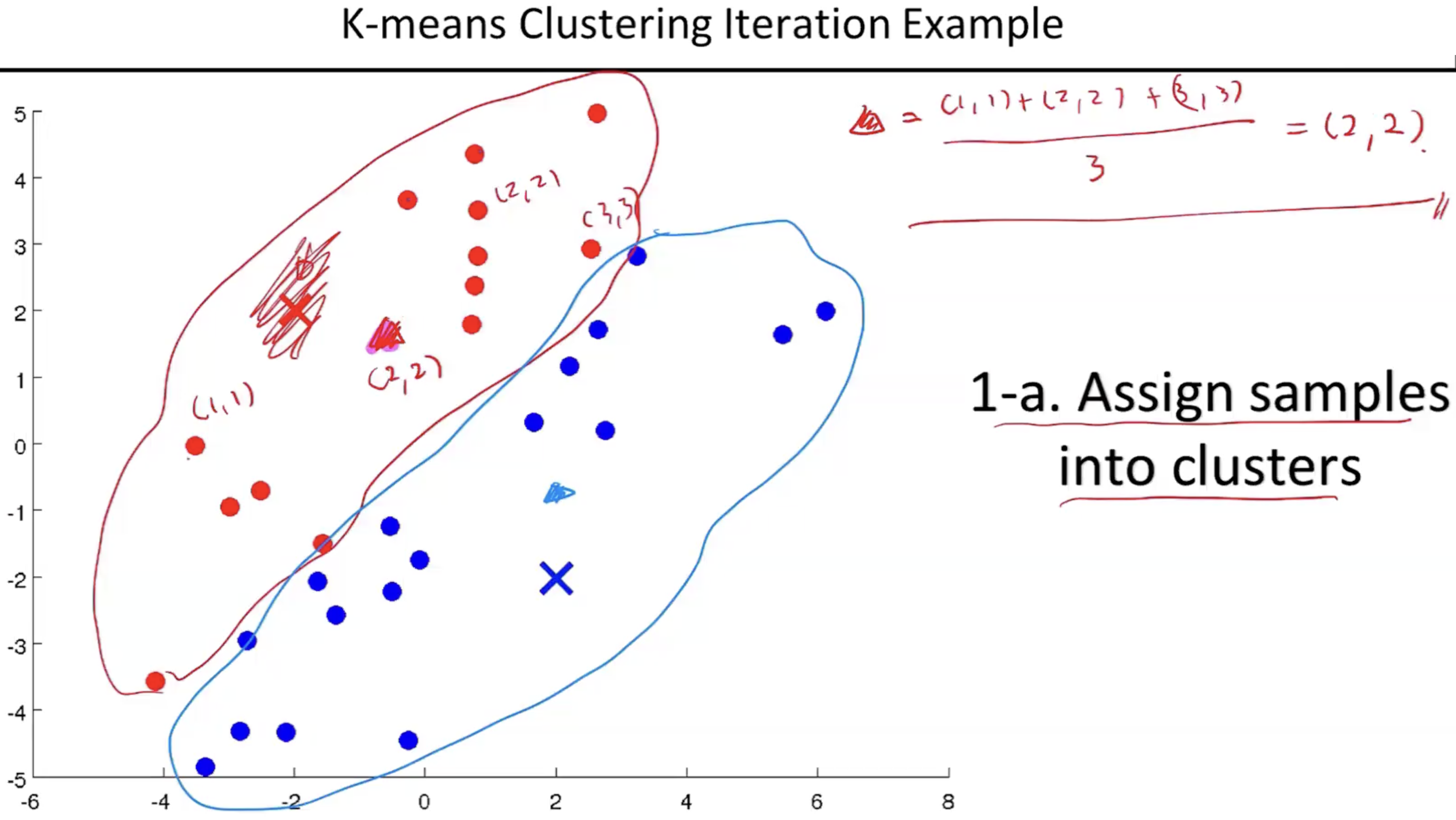
- 그래서 그 다음으로 센트로이드를 우리가 가지고 있는 클러스터에 속하는 데이터들의 평균으로 이동한다. 정확히 말하자면 클러스터 안에 있는 실제 데이터들의 평균위치로 새롭게 클러스터를 정의한다.
- 클러스터에 속하는 데이터들의 평균은 센트로이드와의 거리 평균이 아니라 위치평균으로 계산한다.
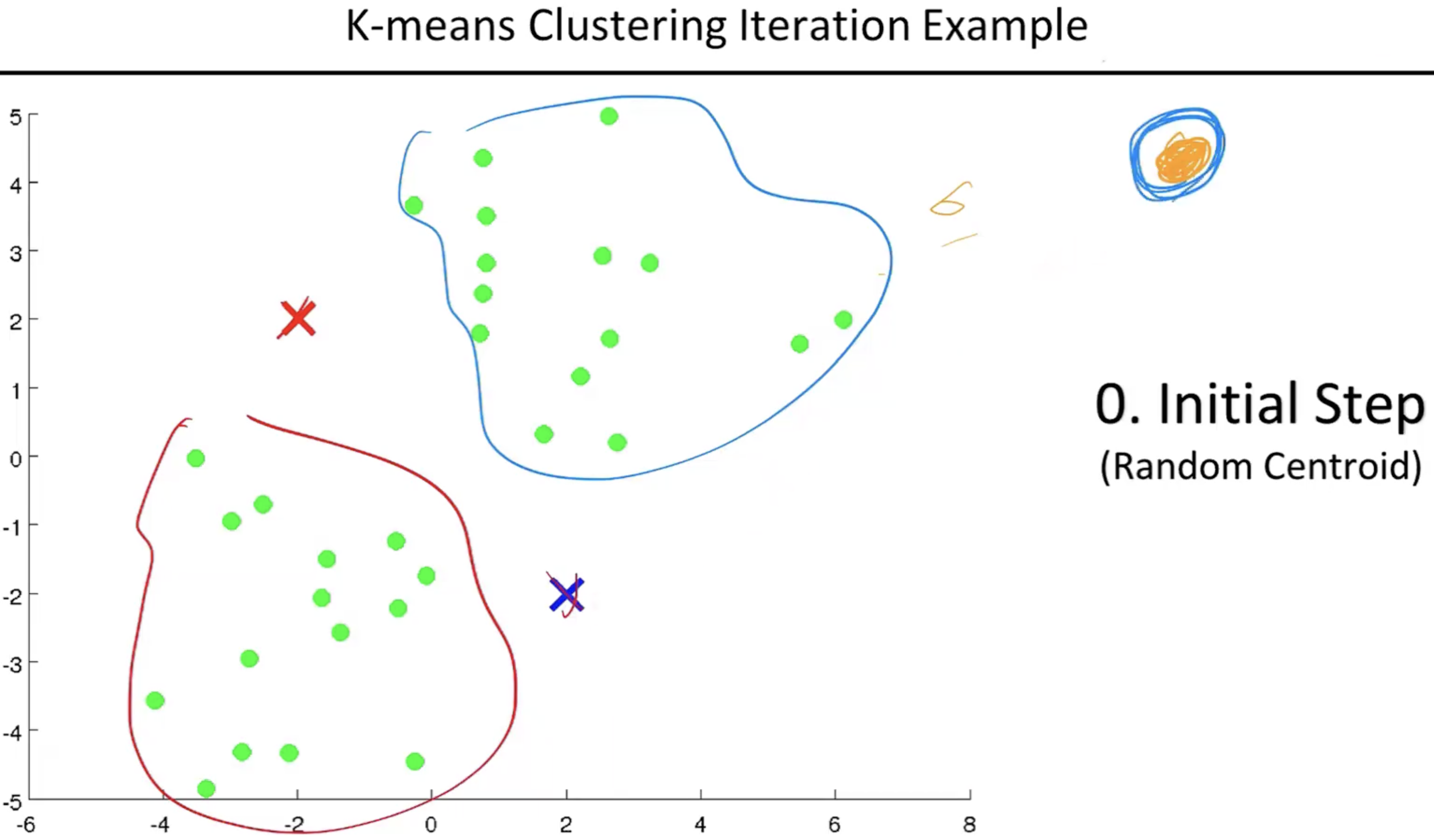
- 새로운 위치로 센트로이드가 정해지면 다시 가까운 데이터들을 다시 클러스터로 만든다음에 속해있는 데이터들의 평균으로 다시 센트로이드를 이동하는 과정을 반복한다.
- 센트로이드가 움직이다가 유의미한 위치로 오는 순간(센트로이드를 옮겼어도 이전의 클러스터랑 동일할때) K-means 클러스터링 알고리즘을 종료한다.

- K-means Clustering을 할때에는 두가지를 확인해야 한다. 첫번째는 데이터가 있으면 이 데이터는 적어도 하나의 클러스터에는 속해야 한다라는 가정을 만족하는 상황에서만 이 알고리즘을 수행해야한다.
- 만약에 outlier와 같은 데이터가 있을때 이상적으로는 노이즈에 속해야하는데 k-means clustering은 무조건 한쪽에 속하여 알고리즘을 계속 진행해야 한다. 이런 노이즈에 속하는 데이터들이 많다면 k-means clustering이 잘 안될 확률이 높다.
- 두번째로는 하나의 데이터는 하나의 클러스터에만 속해야 한다. 중복이 되는 상황에서는 진행이 불가하다.
- 클러스터 사이의 거리가 최소가 되는 클러스터를 찾는것과 결국에는 같은 의미가 된다.

- 다르게 접근하는 방법은 예를들어, 센트로이드가 3개 있다고 가정하고 각각의 데이터들을 랜덤하게 3개의 클러스터로 속하게 assign한 다음 그순간 각 클러스터 기준 센트로이드를 평균으로 찾는다. 이렇게 센트로이드를 찾게되면 아까했던 과정을 반복하여 진행한다.

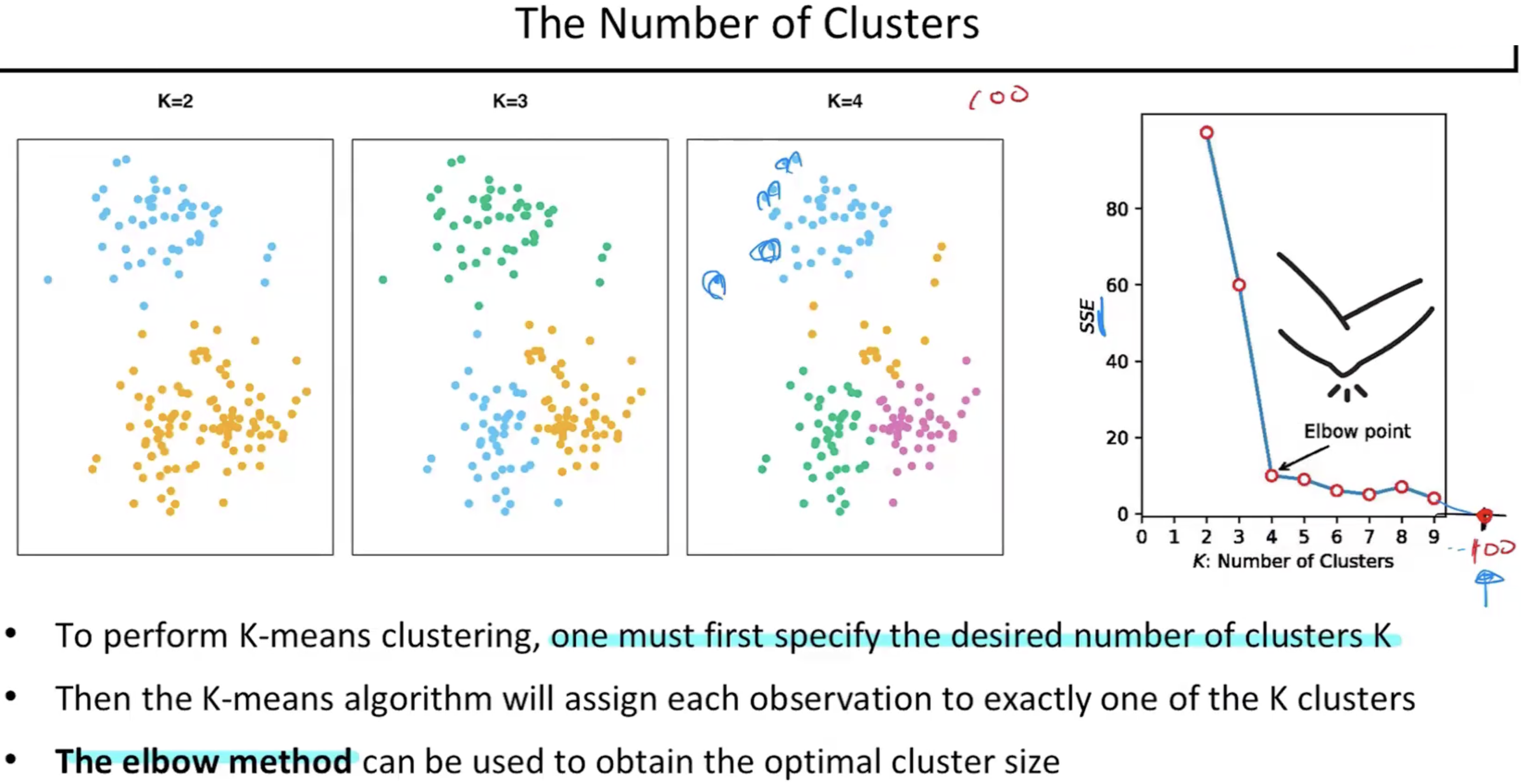
- 그러면 클러스터의 개수를 어떻게 정해야 하는가? 비지도학습이므로 이 데이터에 대한 지식이 없다고 가정하게되면 주어진 데이터에 대한 정보를 메타데이터라한다. 비지도학습은 메타데이터도 없다는게 더 정확한 비지도학습이다. 일단은 찾고자 하는 k에 대해서 하나씩 다 진행해본다. 진행하면서 그래프를 그렸을때 SSE의 값이 확 낮아지는 순간이 있을때 그 위치에 있는 k값을 사용한다. 이것을 Elbow Method라 한다.
- 이후의 k값에서는 과적합의 영역으로 본다. 왜냐하면 만약 데이터의 갯수가 100개 그리고 클러스터의 갯수도 100개라 할때, 그래프에서 k값이 100일때는 SSE값은 0이된다. 모두 각각의 데이터가 하나의 클러스터를 배정하기때문에 최고의 위치가 아니라 과적합의 영역이라고 보는것이다.
- 따라서, 과적합이 일어나지 않을영역에서 최대한의 성능을 내는 위치를 잡고 그 위치를 Elbow point라 한다.
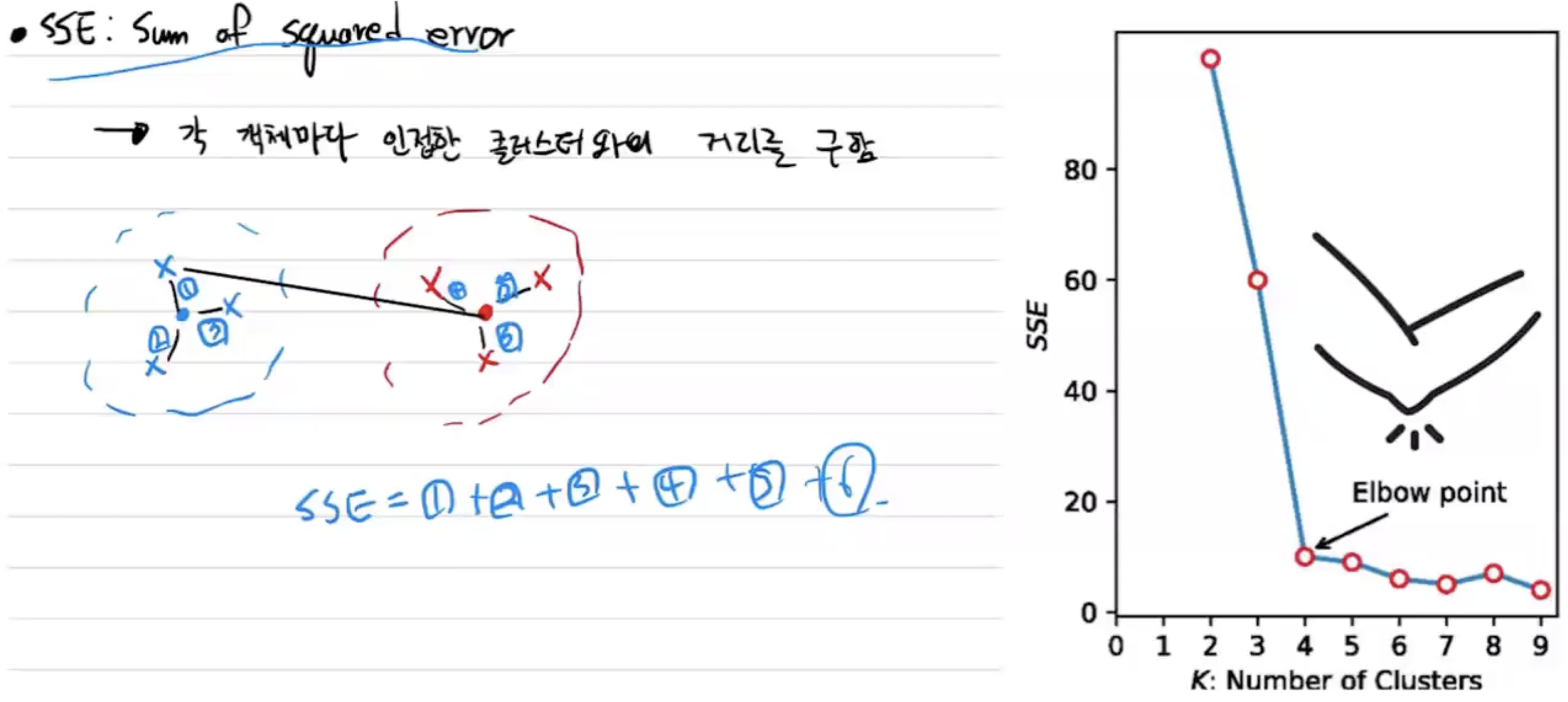
- SSE란 Sum of squred error이라하고 각 객체마다 인접한 클러스터와의 거리를 구하여 합한다.
- 만약 SSE가 크다는 것은 아래 그림처럼 다른 클라스터에 assign이 되어버려서 그 SSE를 계산하는 하나의 거리가 커지는 상황이다.
- k-means 알고리즘도 gradient 알고리즘처럼 운에 따라 initialize가 될때 local optima에 빠질 수 있다. 따라서, 다양한 initialize를 통하여 k-means 알고리즘을 돌려보고 거기서 제일 좋은 솔루션이라고 생각하는 것을 가지고 와서 클러스터링 결과를 사용을 한다.

# Hierarchical Clustering
- k-means 클러스터링에서는 Elbow Method로 k값을 찾아야된다는 기준이 있기에 이걸 원하지 않으면 하이라티컬 클러스터링을 이용하여 최대한 다양한 시나리오를 다양한 군집 시나리오에 대한 도표를 그려놓고 원하는대로 클러스터를 나누겠다라는 컨셉이다.
- 하이라티컬 클러스터링의 결과는 Dendrogram의 형태로 표현이 되고 트리형태이다. 클러스터를 2개든 3개든 나누고 싶을때 맨 위에서부터 클러스터를 나누어서 클러스터링하면 된다. 하나의 Dendrogram을 그려놓고 목적에 맞게 적절한 클러스터의 갯수에 따라 나눌 수 있다.
- 최적의 k값을 주는건 아니지만 적어도 k기준이 정해졌을때 바로바로 잘라서 쓸 수 있다.
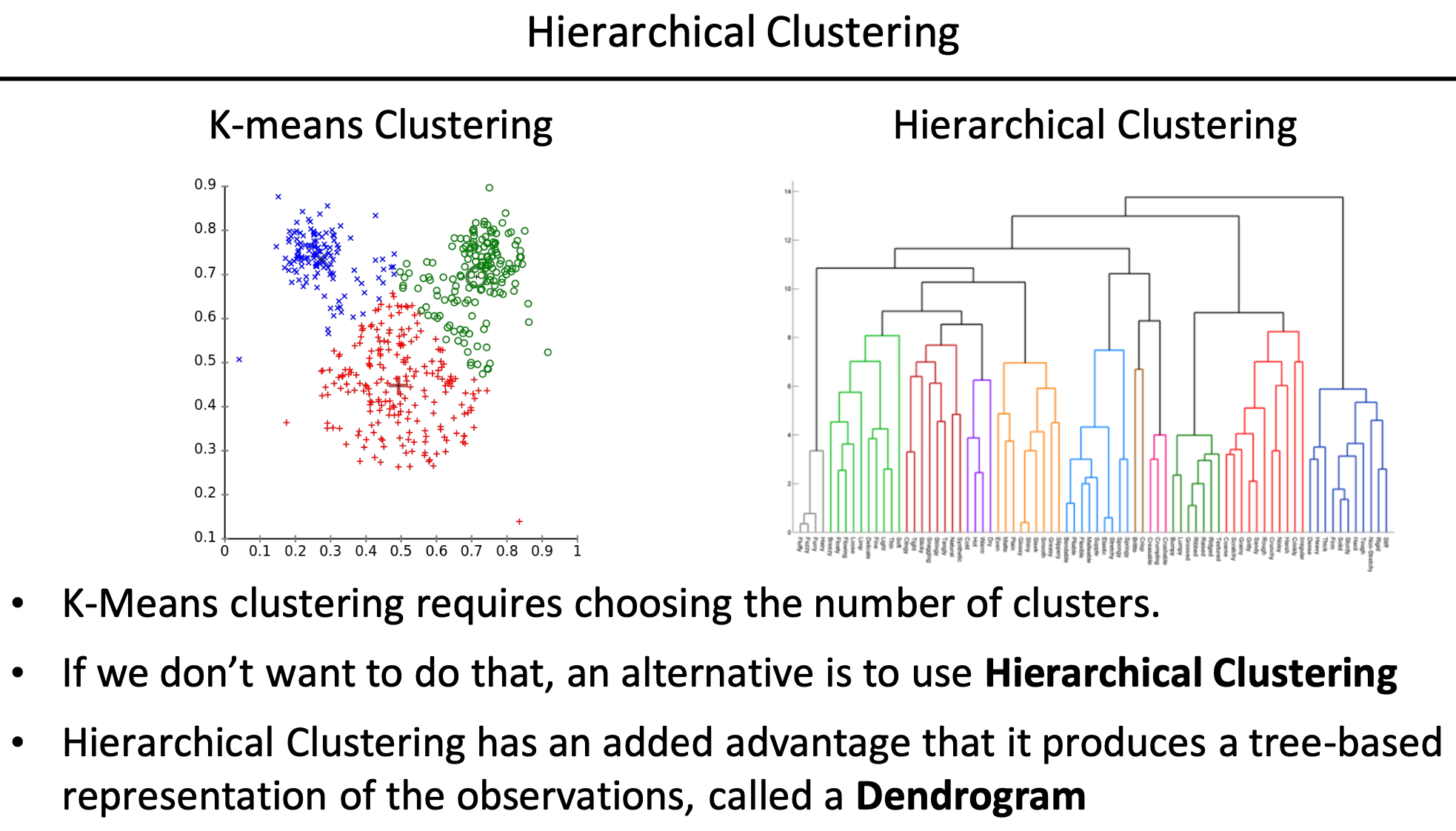
- 모든 데이터 포인트의 유클리드 거리를 잰뒤 가장 가까운 포인트 한쌍을 찾는다. 그 두 포인트를 하나의 클러스터로 본다. 처음보다 하나가 줄은 데이터 포인트로 다시 앞서 거리 잰뒤 또 가장 가까운 포인트 한쌍을 찾아 하나의 클러스터로 묶는과정을 모두 다 묶일때까지 계속 진행한다.
- 다 묶이면 묶이는 클러스터끼리 Dendrogram으로 그리는데 가까운 척도를 높이를 사용하여 그린다.


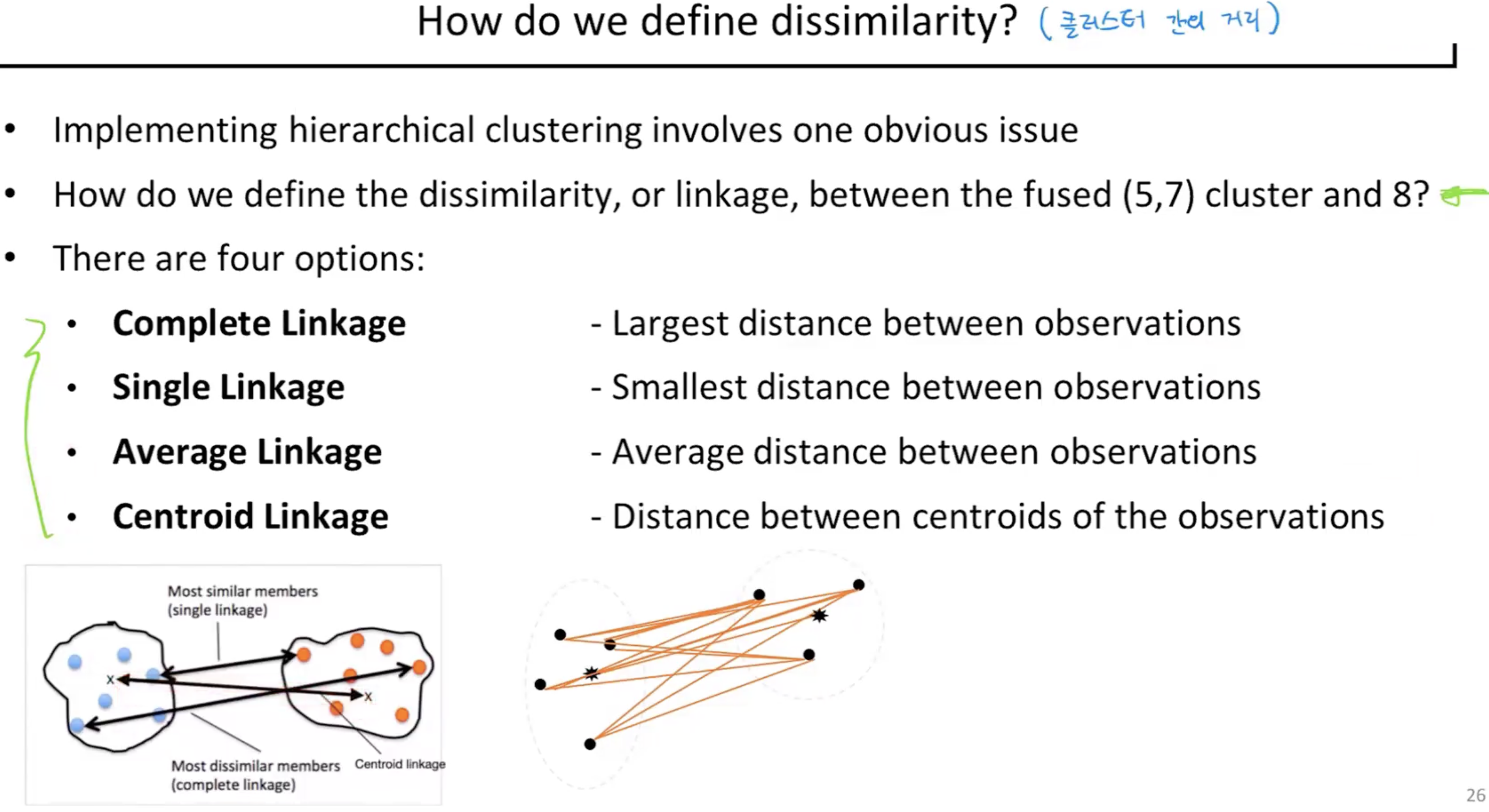
- 두 개의 클러스터간의 거리는 총 4가지 방법으로 잴 수 있다. 첫번째는 두개의 클러스터안에 있는 포인터중 가장 거리가 먼 포인트의 거리를 잰다(Complete Linkage). 두번째는 두개의 클러스터안에 있는 포인터중 가장 가까운 포인트의 거리를 잰다(Single Linkage). 두 클러스터 각각의 평균위치의 포인터들의 거리를 잰다(Average Linkage). Centroid Linkage와 Average Linkage는 같은 의미이다.
- 똑같은 데이터임에도 불구하고 Average Linkage, Comlete Linkage, Single Linkage에 따라 Dendrogram의 결과가 눈으로 봐도 매우 극명하게 다른다는것을 알 수 있다.
- 그러면 어떤 기준으로 선택해야 되냐? Average Linkage, Comlete Linkage는 균등하게 분포하는 경향이 있는반면에 Single Linkage는 조금 극단적인 클러스터를 만드는 경향이 있다. 따라서, 어느것이 맞고 틀리다라고 말할 순 없지만 데이터에 outlier와 노이즈가 많다면 Single Linkage를 쓸수도 있고, 데이터를 잘 모르겠거나 균등하게 클러스터링 된거 같으면 Average Linkage, Comlete Linkage를 사용할 수도 있다.

- dissimilarity measure을 잴때 거리를 재는 기준만 계속 달라지지(어떤것을 선택하냐의 차이였지) 결국에는 선택을 하고나면 그들간의 L2거리(유클리드거리)를 봤을때 그 값 자체가 중요하지 않는 상황이 있을 수도 있다는 말이 아래 그림이다.
- 실제로 그 값들간의 차이 유클리드 거리를 기준으로 예를 들어보면 주황색선과 분홍색선이 훨씬 더 가깝다고 할 수 있다. 그러나 자세히보면 주황색선과 초록색선의 추세를 보면 모양이 매우 닮아있다. 따라서 주황색과 분홍색이 가까운지 주황색과 초록색이 가까운지는 어떤 데이터를 다루느냐에 따라서 많이 달라진다. 예를들면, 주식의 그래프로 봤을때 주황색과 초록색은 더 연관성이 있다고 말할 수 있다.
- 이런 알고리즘을 십분 활용하려면 데이터에 맞게 거리라는 기준을 어떻게 정하는가는 배워서 하는 영역은 아니고 데이터를 보고 능동적으로 선택을 해야되는 영역이 된다.

- Dendrogram에서 맨 아래에 있는 데이터가 가장 가까운 클러스터이고 점점 위로 올라갈수록 멀어지며, 가장 끝쪽에 있는 하나의 데이터 포인트를 leaf라고 한다. 트리구조에서도 일반적으로 leaf라고 부른다.

'yeardreamschool4 > Machine Learing' 카테고리의 다른 글
| Multi-Class Classification Model (0) | 2024.05.24 |
|---|---|
| Binary Classification Model(이진 분류 모델) (0) | 2024.05.23 |
| Dimension Reduction(차원 축소) (0) | 2024.05.22 |
| Logistic Regression(로지스틱 회귀) (0) | 2024.05.20 |
| Linear regression(선형 회귀) (0) | 2024.05.20 |



